08 de Noviembre de 2012
Fracciones Algebraicas
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.
Son fracciones algebraicas:
Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.
El valor de una fracción no se altera si se multiplican o dividen el numerador y denominador por una misma cantidad. Esta cantidad debe ser distinta de cero.
Las fracciones algebraicas tienen un comportamiento similar a las fracciones niuméricas.
Operaciones con fracciones algebraicas
Simplificar fracciones algebraicas
Suma y resta de fracciones algebraicas
Para sumar y restar procederemos de forma similar que con fracciones de números enteros, reduciendo primero a común denominador.
Producto de fracciones algebraicas
Para multiplicar fracciones algebraicas procederemos igual que con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Cociente de fracciones algebraicas
Para dividir fracciones algebraicas procederemos igual que con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Ejemplos: Cociente de fracciones algebraicas
- Opera:
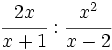
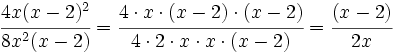
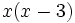
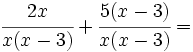
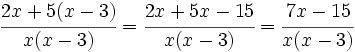
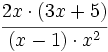
Simplificamos antes de efectuar el producto:
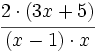
Finalmente, podemos multiplicar, si es preciso:
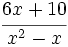
4.Solucion:
Hacemos el producto cruzado, dejándolo indicado:

Simplificamos:
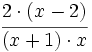
Finalmente, podemos multiplicar, si es preciso:
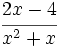
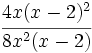
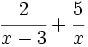
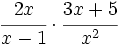
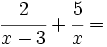
No hay comentarios:
Publicar un comentario